NotesFrom a Small Universe

A Warp in Time

In the previous chapter we were introduced to Einstein’s Theory of Special Relativity and how it made lengths of space and time relative quantities that could appear different to different observers.  The concept of light plays a central role in Special Relativity.  In this chapter we ask the question ‘what type of energy does light have’?  In answering this question, Einstein showed using his new theory that mass is a form of energy and the two can be converted between.  To see this we will need to introduce something called a space-time diagram, which is a simple way of depicting an object’s path through space.  We will then see the effects that massive objects have on space-time using General Relativity, the theory Einstein spent a decade working on after his publication of Special Relativity.

Types of Energy

Very broadly there are two types of energy: kinetic energy and potential energy.  Kinetic energy is the energy that a moving object has.  The amount of kinetic energy an object has depends upon how massive it is (that is to say, how heavy it is) and how fast it’s moving.  A car going at twenty miles per hour has more kinetic energy than a tennis ball going at twenty miles per hour because although the two objects have the same speed, the car obviously weighs a lot more.  And similarly, a car going at a hundred miles per hour has more kinetic energy than a car going at twenty miles per hour because although the two objects weigh the same one is travelling much faster.

The second type of energy, potential energy, comes from separating two objects that have a force trying to bring them close together, or conversely from putting together two objects that have a force trying to separate them.  For example, the Earth’s gravitational pull means that all objects try to fall down to the centre of the Earth.  Because the ground is stopping you getting to the centre of the planet, you have a certain amount of potential energy.  And if you were to be raised high up into the air, in a skyscraper or a plane say, you would have a lot more potential energy because you would be further from the centre of the planet.

For an example of the opposite effect we could use two bar magnets.  Imagine we point them so that their two south poles are facing one another.  The two magnets will then be trying to repel each other- to create as much separation as they can.  If we push them closer and closer together they gain more and more potential energy.

Energy is often stored in the form of potential energy, either in man made products such as batteries or in naturally occurring ones such as diesel.  I’ ll just use a frivolous example to show how this can work.  Imagine having a heavy metal ball on a raised platform.  The ball has potential energy from being raised above the ground but the platform acts as a barrier stopping it falling.  By supplying a certain amount of energy to remove the platform (by pushing it aside, for example) the stored potential energy is released and converted into kinetic energy as the ball falls to the ground.  I suppose as it lands the ball could trigger some useful device in a Rube Goldberg type contraption, so in that way we could claim the setup was storing energy for a useful purpose.

In diesel the principle is much the same although the potential energy is supplied by electrical rather than gravitational potential.  The atoms making up the diesel have positive and negative charges creating a complicated setup of attraction and repulsion.  The whole group could be rearranged into a new state with less potential energy thereby releasing that potential energy for useful purposes, but it takes a certain amount of initial energy to set this reaction going (analogous to the energy required to move the platform), this energy is supplied by heating the diesel.

Conservation of Energy

Energy can be converted between different forms.  As we saw with the ball on the platform, potential energy can be converted into kinetic energy.  And obviously kinetic energy can be exchanged between objects: if one pool ball hits another one then the moving ball slows down and the stationary ball speeds up.  But energy can only be converted, not created or destroyed. The reason for this reveals to us something deeply fundamental about our universe: the fact that the laws of physics are unchanging, they are the same today as the always were in the past and always will be in the future.  Let& rsquo;s illustrate this with an example.  Imagine watching a video of a ball being dropped from the top of a metre rule which allows us to calculate the ball’s speed as it falls.  Imagine if the laws of physics were not unchanging, but instead as time went on the laws of physics changed so that objects were imbued with additional kinetic energy as time progressed.  The ball would fall faster the later in time it was dropped and keep gaining speed throughout its drop due to the additional kinetic energy it gained.  Just by watching the video and calculating the speed of the ball we could determine the date on which the video was made.  This is evidently not the universe which we live in.  In that example, energy was obviously not being conserved because the ball’s total energy changed (at any point in the drop, the ball’s potential energy would be determined by its height above the ground and its kinetic energy by the ball’s speed, which as we said was changing). In 1915 the mathematician Emmy Noether proved that if any law of physics changed over time then energy would not be conserved [A].

Noether’s theorem also shows the conservation of quantities other than energy arise from fundamental facts about our universe.  For example, momentum is conserved and this tells us that the laws of physics are the same across the whole of space.

What Type of Energy Does Light Have?

Light obviously carries some sort of energy.  We experience this every day when the light from the sun reaches us, we feel the energy on our skin as heat.  We could convert the energy from sunlight into other forms if we wished, such as using solar panels to convert it into electrical potential energy.  But what type of energy does light itself have?  It doesn’t fit our definition of potential energy- it has nothing to do with separating objects that are trying to approach one another or vice versa.  So can light carry kinetic energy?  At the beginning of the 20th century the answer again would have been no, light didn’t have any mass- it didn’t weigh anything- so it couldn’t have kinetic energy (as we saw above, the lighter an object the less kinetic energy it carries and if it has no mass it carries no kinetic energy).  This line of thinking changed radically in 1905 when Einstein showed that mass is a form of energy itself, and since light carries energy it is equivalent to say that it has mass.  We’ll follow through his line of reasoning [1].

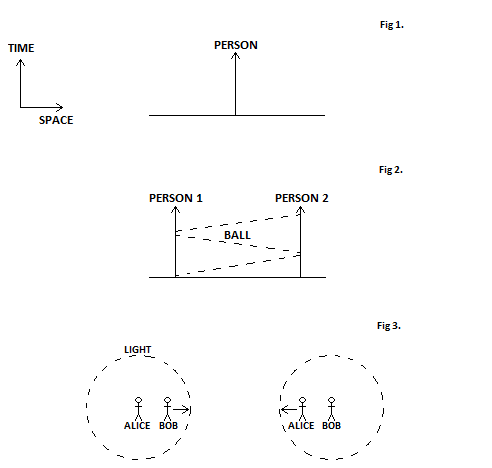
We start with a ball floating in empty space that at one instant radiates out a pulse of light equally in all directions.  We then imagine a giant sphere enclosing this ball (see Figure) and also enclosing the light it emitted.  The sphere therefore encloses a certain amount of energy, in total this will be the energy of the light enclosed and the energy of the ball itself, which must all be potential energy between the atoms that make up the ball since the ball itself is not moving and it therefore has no kinetic energy.

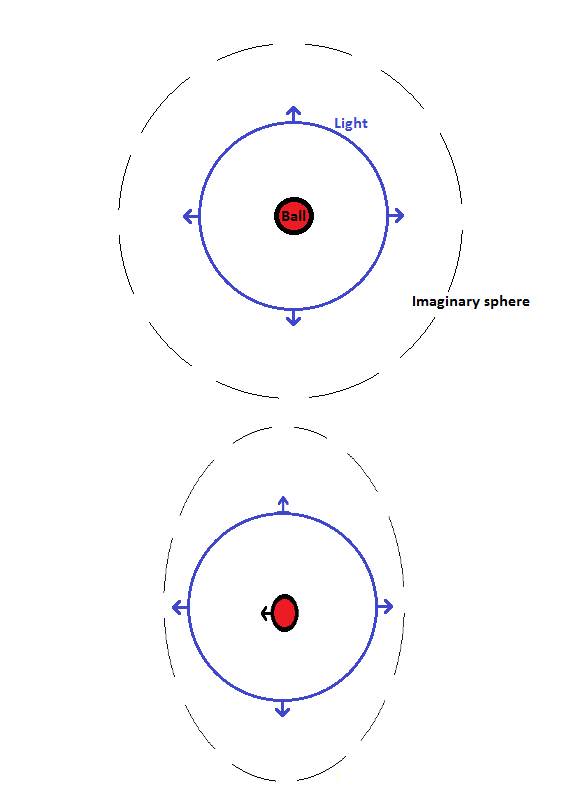
Top: A ball emits light in all directions and this system is contained within a sphere.
Bottom: From the point of view of our friend, the whole system is moving. The 'sphere' is length contracted so it is oblate. The system is therefore contained in a smaller volume and the light is more intense.

Now imagine how this whole system looks to some friend who is travelling past the outside of the sphere at a fast speed, some appreciable fraction of the speed of light.  As we saw in the previous chapter, light travels at the same speed regardless of how fast you are moving.  So our friend still sees the light expanding from the ball equally in all directions at the speed of light, and the light emitted by the ball is still contained within the sphere.  However, another consequence of Special Relativity is relevant here: length contraction.  Because our friend is moving, the length of space is squished in the direction that they are travelling (see Figure).  From their point of view the sphere is not truly a sphere, but is oblate.  The surface area of this new shape must be less than that of the sphere, since it has become reduced in one direction.

According to our friend, the light is enclosed in a smaller volume.  That means that the light must be more intense: our friend sees each light ray as carrying more energy than we do.

Since we are not moving relative to the ball, it has only potential energy and no kinetic energy.  When the ball emits a pulse of light in all directions this light carries away a certain amount of energy.  Since the energy must come from somewhere it must be provided by the ball, so the potential energy of the ball must be reduced as it emits light.

For our friend who is moving past the ball at some speed, the ball has not only potential energy but also kinetic energy.  As the friend sees it, when the ball emits the pulse the light carries away more energy.  In order to make up the difference and conserve energy, the kinetic energy of the ball must reduce and this means either the speed or the mass of the ball must reduce.  The speed cannot reduce because if the ball slowed down from our friend’s point of view it would have to start moving in our point of view, and it cannot do that because it is emitting light equally in all directions so there would be nothing that could make it go in one direction rather than another.  If the speed cannot reduce then it only leaves one option: the mass of the ball must reduce.  We have shown that because the ball lost energy it lost mass.  Therefore we can translate between mass and energy.  This means that light, which carries energy, has an equivalent mass and therefore an equivalent kinetic energy.  In fact, a tiny amount of mass is equivalent to a huge amount of energy.

Space-time Diagrams

We saw in the previous chapter that space and time are both warped by movement and in opposite ways, time gets lengthened (making a clock tick slower) and space is contracted (making a measuring rod shorter), and we know that the two effects are linked.  The best way to visualise this in a space-time diagram.  This is just a simple diagram with time going up the page (the y-axis) and distance in space going along the page (the x-axis).  Usually, only one space dimension is shown in a space-time diagram rather than the three that exist in real life since it makes it much easier to draw on page and still gets across all of the important points.

So, a stationary point in space, say representing a point where a person is standing, will mark out a vertical line on the space-time diagram like this (Figure 1).

Let’s draw the diagram for two people standing still and throwing a ball back and forth.  The two stationary people would mark out two vertical lines and the ball tossed between the two of them would mark out diagonal lines between the two people as it moved through time (Figure 2).

The angle that the diagonal line makes with the people’s vertical lines depends upon the speed at which the balls is thrown, the faster the ball travels the greater the angle, so if the ball could move instantly between the two places it would be a horizontal line of 90 degrees.

Let’s consider the following thought experiment.  We have an astronaut called Alice floating in empty space.  Another astronaut called Bob is approaching her with a certain speed.  At the very moment that Bob passes Alice she presses a button on her beacon and sends out light-beams in all directions creating a sphere of light around her that spreads out.

From Alice’s point of view she is at the centre of an expanding sphere of light while Bob continues to move away from the centre.  But since Bob was next to Alice when she pressed the button on her beacon, and since no matter what speed he has relative to Alice he will see the light spreading out from him at the same speed in all directions (just as the speed of light was the same in all directions regardless of whether it lined up with the movement of the Earth or not in Michelson’s experiment earlier in this chapter).  This means that from Bob’s point of view he is at the centre of the sphere of light while Alice moves away from the centre. (Figure 3).

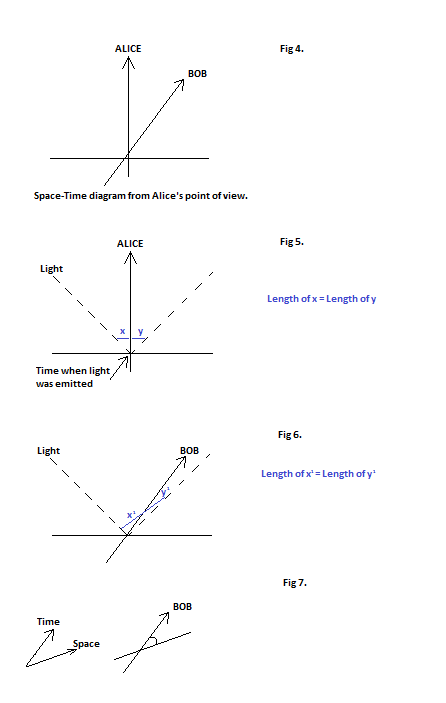
In order to see how to resolve this paradox it is best to draw the lines of both Alice and Bob on a space-time diagram.  If we draw Alice as staying still then her line will move vertically up the diagram while Bob’s line will be a diagonal since he is moving through space with a constant speed. (Figure 4).We could call the line labelled ‘Alice’ the time-axis from Alice’s point of view and the line labelled ‘Bob’ the time-axis from Bob’s point of view.  It is, from their own point of views, the line where they stay still in space and move only through time.

Now let’s draw on a line representing the edge of the sphere of light as it spreads out.  The light beams spread out from Alice in all directions in space (in this diagram just two directions as we are only showing one space dimension), the beams travel with a certain speed which we define as a 45 degree angle from Alice’s vertical line.  Because they are travelling with the same speed in both directions, at any particular instant (any horizontal line across the time axis) the two beams will have travelled the same distance.  Now, Alice is at the centre of the sphere so the beams must extend the same distance to either side.  If we start with Alice in the centre and draw to lines of equal length, one out to each beam, we see we have drawn a line parallel to the space axis.  In fact, we can use this line, which connects to two sides of the light sphere, as defining the space-axis. (Figure 5).

Now let’s consider how the sphere of light must look from Bob’s point of view.  We have already determined that he also sees himself at the centre of the light sphere, so we pick two points on the light rays that put Bob at the centre.  We can see that this is a diagonal line on the diagram, rather than a horizontal line like it was for Alice.  Like we did before with Alice, we can use the light sphere to define the space-axis as Bob would see it. (Figure 6).

What we can see is, while for Alice, who is stationary, the space and time axes are at 90 degrees, for Bob, who is moving, the space and time axes have an angle less than 90 degrees. (Figure 7).

Of course, from Bob’s perspective he is the one who stays still while Alice moves.  So if we wanted to redraw the whole thing from Bob’s perspective, we would need to deform the paper so that his space-axis and time-axis were at right angles.  Of course, this deformation also means that Alice’s space-axis and time-axis are no longer right angled.  What we can see is this: from your own viewpoint you are always stationary (you don’t move relative to yourself) so if you were to draw a spacetime diagram the two axes (space and time) are at 90 degrees to one another. But, for any observer who is moving relative to you their axes (their perception of space and time) no long appear to you to be at 90 degrees to one another.  The time dimension has expanded into the spatial domain.  We see that spacetime is quite a malleable entity that can deform depending on your state of motion.

General Relativity

Special Relativity is a remarkably successful theory but one with limited scope.  It says that two observers that are not accelerating with respect to one another will always agree on the results of an experiment.  But what of observers that are accelerating with respect to one another?  This is a particularly poignant question since gravity causes acceleration- here on Earth all objects are accelerated towards the centre of the planet.  Even though the effects of gravity are often weak enough to ignore for practical purposes from a fundamental viewpoint it is clear that Special Relativity is missing a key part of our universe.  General Relativity is Einstein’s theory of gravitation that describes how to do physics in accelerated frames, developed over roughly a decade following the publication of Special Relativity.

General Relativity is a strange theory in that although the maths underpinning it is notoriously difficult to get to grips with the concepts underpinning it are beautiful in their simplicity.  Imagine a person standing at the top of a tall ladder to paint a house, holding a pot of paint and a brush.  Suddenly the rung the person is stood on breaks and the unfortunate painter finds themselves falling towards the ground.  As the rung snaps the painter drops the brush and paint pot in surprise.  Ignoring small details such as air resistance and spin, which of the three objects -the painter, the brush and the pot- will hit the ground first?  The answer of course is that they all land at the same time.  Even though the person is a good ten to a hundred times heavier than the other two objects, all objects fall at the same rate. This fact had been known since by Galileo, but almost three hundred years later, Einstein would be the first to understand on a fundamental level why this was the case.  

The Equivalence Principle

The key insight that Einstein had on this situation was that from the point of view of the person in free fall there is no gravitational field, the brush and the paint pot and any other object will fall at the same rate so they will just hang next to the painter exactly as if there was no gravity (until they all hit the ground of course).  If you were to awake one day in a large, perfectly sealed box, and you held a ball out in front of you and let it go and the ball just hung in the air you wouldn’t be able to tell if there was no gravitational field (for instance if the box were in deep space far from the influence of any stars) or if the whole box was in a gravitational field but falling at a great height so that the ball, yourself and the box surrounding you were all falling at the same rate.

In the opposite scenario if you let go of the ball and it did drop you wouldn’t be able to determine if the box was sat on the ground in a gravitational field or if there was no gravitational field but the box was being accelerated upwards, so that the floor of the box was rising to meet the ball.  In this way there is a perfect equivalence between a gravitational field and an accelerating reference frame- the strength of a gravitational field is relative to the movement of an observer.

Consider a rocket sat motionless in empty space.  The rocket has a window on the Western side near the top of the ship and a window on the Eastern side near the bottom of the ship (see Figure).  A light ray that enters straight through the Western window will not exit by the Eastern one because they are out of line, the light ray will be shining on the interior Eastern wall above the window.  What happens when the rocket fires its thruster?  The rocket is now accelerating upwards.  As the light ray enters the Western window the rocket moves skyward so that by the time the light ray has crossed the interior of the ship the Eastern window is now in the light ray’s path and the ray exits through the window.  From the point of view of a passenger onboard the rocket, the light ray has travelled along a bent path, entering near the top of the ship and curving downwards so that by the time it has crossed the interior it is near the bottom of the ship.  The faster the acceleration of the rocket the more the light ray’s path is bent.

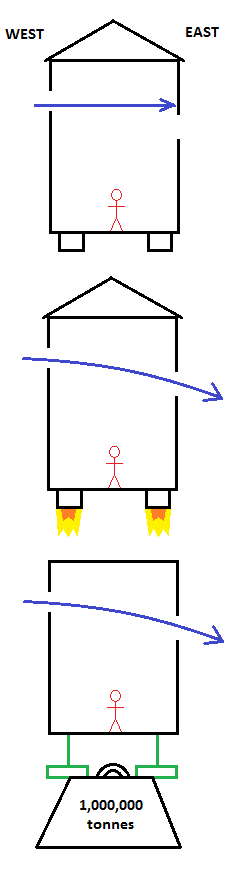
Top: When the rocket is stationary, the light enters the western window and strikes the wall since the windows are out of line.
Middle: When the rocket is accelerating, the path of the light ray is curved so it can enter the western window and exit the eastern window.
Bottom: From the equivalence principle, the same effect occurs in a gravitational field. The rocket could be on supports and gravity bends the light ray. If the person in the ship couldn't see out of the window to see if they were moving they would have literally no way of knowing if they were in the middle situation or the bottom one.

From our equivalence principle we can say that a light ray’s path would also be bent in a gravitational field, and the path would become more bent the stronger the gravity was.  In fact this was one of the major predictions of General Relativity- that a light ray would be bent far more by gravity than under Newton’s theory of gravitation. & nbsp;This prediction was proven true by two expeditions led by Arthur Eddington in 1919 to observe solar eclipses in Brazil and Principe, an island off the coast of Africa.  When a solar eclipse happens and the moon passes in front of the sun, the sun’s light is blocked out so that the stars become visible as they are at night.  However, if you look up at the stars at night the sun is beneath your feet and hidden behind the Earth while during an eclipse if you look up at the stars , the light from those stars passes next to the sun in order to reach you. (If you do get the chance, it’s not a good idea to try to observe a solar eclipse directly with the naked eye).  According to General Relativity, the gravitational field of the sun can affect light, the path of the starlight becomes bent and positions of the stars in the sky become offset from their usual positions. This was indeed what Eddington’s expeditions observed.  While General Relativity had already had success in explaining deviations in the orbit of Mercury (which of course is the closest planet to the Sun and therefore feels its gravitational effects most strongly) this was the first major test of the theory on new data and also vindicated the equivalence principle that there is no difference for an object at rest in a gravitational field and an object accelerating in the absence of a gravitational field.

Curving Space-time

Let’s consider the worldline (the path on a space-time diagram) of an object at rest.  It is of course a straight line (see Figure), as by definition at any point along the time axis the object is at the same position.  What about the worldline of an accelerated object?  The straight line now becomes a curve because as equal time intervals pass larger distance intervals are travelled.  From the equivalence principle we can say that an object at rest in a gravitational field would have exactly the same curved worldline.  How do we transform from the straight wordline of an object in empty space to the curved worldline of an object in a gravitational field?

It is the same as drawing a straight line on a curved surface.  For example consider taking a straight piece of string and trying to fix it flush against the surface of a football.  There’s no way for the string to be on this surface and still remain “straight” because the surface its attached to is curved.  Similarly, the worldline of an object can no longer remain “straight” in the presence of a gravitational field because the spacetime through which the worldline is drawn is curved.  In this way we could say that gravity curves spacetime.  Perhaps a better way of saying it when you look at the mathematics of General Relativity is that gravity is curvature in spacetime.  If empty spacetime could be viewed as a flat sheet extending infinitely in all directions, then if a mass such as the sun or the Earth were placed the sheet all around that mass would curve.

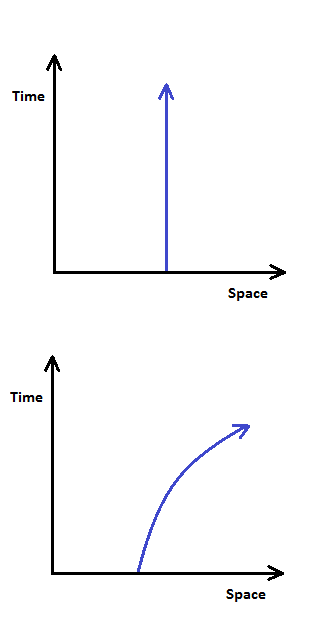
Top: The worldline of a stationary object; it does not move in space.
Bottom: The world line of an accelerating object; it travels larger distances in space as time increases. From the equivalence principle, the worldlines of objects in a gravitational field curve in the same manner: straight lines become curved.

Perhaps the most profound result of General Relativity is that spacetime is now a malleable entity.  Not only does it have an effect on physical objects by curving their paths but in turn the physical objects have an effect on spacetime by causing it to deform.  This is why the path of light from stars is altered during an eclipse: the space that they have to travel through is being curved by the strong gravitational field of the sun so the paths that the light traces is also curved.  In fact the curvature of spacetime around a dense gravitational field like that of the sun is similar in shape to the curvature of glass in a lens.  For that reason the curving of light in this way is called gravitational lensing and is an increasingly important tool in astronomy because, like regular lensing, gravitational lensing increases the magnification and brightness of the objects it focuses.

Although we have only really talked about space being curved in the examples above, it is of course space-time which is being curved (since we saw the merging of the two in the previous chapter) .  So not only does space become warped in a strong gravitational field but time becomes stretched out also, meaning that the passage of time is slower the nearer you are to a strong source of gravity such as a black hole, the sun or even the Earth.

This stretching out of time is another form of time dilation, like that caused by Special Relativity.  But there are subtle differences.  In Special Relativity, two observers both move relative to one another and so they both see the other person’s clock slow down.  By contrast, in General Relativity, both observers would agree that if someone went close to a black hole or any gravity source, that person’s clock would slow down.  The two observers agree because in General Relativity space-time is a malleable entity which has become warped in a particular area due to the effect of gravity.

In Special Relativity, the time dilation and length contraction are a consequence of relative movement.  General Relativity introduces an additional source of time dilation and length contraction: the warping of space-time.

There is one more fact that is not only very interesting but also very important to hold in mind while reading the rest of this book  If gravity is the curvature of spacetime what causes gravity?  It is well known that mass causes gravity but as we saw, mass is just a form of energy.  So all energy contributes to the bending of spacetime.  A photon of light curves space-time, even though it has no mass in the conventional sense, since it carries energy.  (The curvature is very small since the energy carried by a photon is generally less than the mass-energy of even a tiny particle like an electron.  So the gravitational force provided by a photon is less than the gravity of even a single electron.)  If an object like a battery is charged (so it has more potential energy) it curves spacetime more than if it is not charged.  But these effects are so tiny that they are only observable in the most exceptional of circumstances.  

How space-time is curved is dependant on all of the energy acting on it including the energy of photons, potential energy and pressure from gas and dust.  These factors can cause the curvature of spacetime and also cause it to expand or contract with time.  We don’t have to confine ourselves to the space-time of the relatively small patch of universe around a star, we can consider the space-time of the universe as a whole.  As we shall see later, it is these changes in space-time that govern the evolution of the cosmos.

Whether Ether

I’ve implied when writing this chapter that Einstein’s main motivation for developing Special Relativity was to explain the result of the Michelson-Morley experiment but this is a bit misleading.  Einstein went from pretty much total obscurity in the physics world to publishing his theory so there is not much on record in the way of notes and correspondence to shed light on what he was thinking as he developed the theory.  Einstein himself claimed that the Michelson-Morley experiment didn’t have a substantial influence on his thinking during the work.  It is worth noting that explaining the Michelson-Morley experiment, along with several other experiments in the same vein, were a big puzzle in theoretical physics at the time and many of the foremost physicists were working on it.  No work exists in a vacuum, much of Special Relativity was laid out by various physicists other than Einstein.  What Einstein did was bring all of the existing ideas and mathematics together, derive all of the results from two very simple postulates and to explain physically what it all meant.

(Before Einstein’s Special Theory of Relativity, the physicist Hendrik Lorentz actually developed a theory whereby physical objects could push ether along.  So, for example, the Earth would push and drag ether around with it in the planet’s orbit around the sun, explaining why the Michelson-Morely experiment couldn’t detect the motion of the ether: the ether moved along with the Earth.  But there was a big flaw in this theory: from Newton’s Laws the ether should create a reactionary force on the Earth and slow it down (equivalent of air resistance, effectively).  This obviously isn’t observed; the Earth isn’t slowing down in it’s orbit.  In this way ordinary matter like the Earth could affect ether by dragging it but ether couldn’t affect ordinary matter by slowing it.  Interestingly, the reason Newton eventually dismissed a wave theory of light and leant towards a particle theory was that if light was carried by an ether then this ether would produce a drag on planets and comets [2].  This is a duality problem much like the mind-body duality problem we talked about in the previous chapter, where if we assume an ethereal spirit for the mind that isn’t bound by physics, then the mind can interact with ordinary matter but the ordinary matter cannot interact with the mind.  Although Lorentz’ theory adequately explained contemporary experimental results on a mathematical basis, on a physical and philosophical basis it was less than satisfactory.  These tensions were removed with the understanding that Einstein’s theory brought.)

So what was Einstein’s motivation?  It’s hard to say but it seems that his key motivation came from Maxwell’s equations of electromagnetism.  Einstein was very fond of the idea that you can only define motion relative to another body, and not in any absolute way that holds everywhere in the universe.  But Maxwell’s equations, which were and are one of the triumphs of physics, describe how electromagnetic waves, such as light, propagate through ether, and if this ether is unmoving then you could define absolute motion relative to this stationary ether.

Maxwell’s equations [B] describe a wave motion travelling along like a wave in the ocean.  Every time an electric wave moved, up or down, it would generate a magnetic wave at right angles, and the magnetic wave would generate an electric wave, and so on.  But what happened if a person could sit on top of the peak of an electric wave and move along with it (see Figure)?  Einstein realised that from the point of view of this person, the electric wave is not moving (in the same way a train doesn’t appear to be moving if you are on the train).  And if the electric wave is not moving then no magnetic wave is generated.  For this person, travelling along at the speed of light, time has come to a standstill.  In recognising that time must come to a halt for someone travelling at the speed of light, and in tying together the mathematics of previous works by Lorentz and others, Einstein developed Special Relativity.

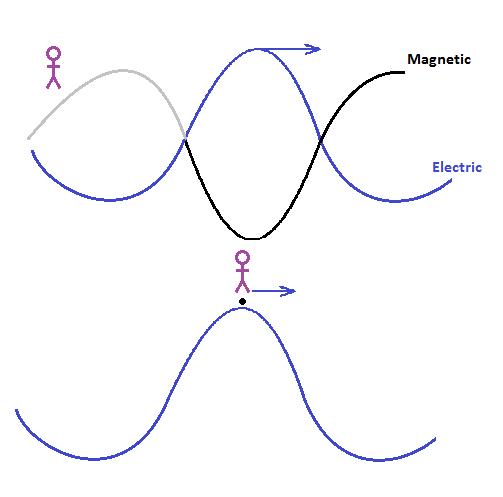
Top: The movement of the electric wave causes the magnetic wave.
Bottom: If a person sits on the electric wave and moves with it they don't see any movement in the electric wave and therefore see no magnetic wave.

Of course, not matter what Einstein’s motivation was, the Theory of Special Relativity had a profound impact on explaining the results of the Michelson-Morley experiment.  To recap briefly (and feel free to flick back to earlier in the chapter if you need to refresh yourself on the details), the experiment had set out to show the effects of ether by looking for a slight difference in the speed in two light rays, one sent out forwards from the experimenter and one sideways.  The result of the experiment is that both light rays travel at the same speed.  If the light rays are being carried by the ether, this is only possible if the apparatus is not moving with regards to the ether.  Imagine that we have two observers, Alice and Bob, moving at great speeds relative to one another and both of them perform the experiment.  From Special Relativity’s second postulate, that the speed of light is the same, both Alice and Bob will find their own light rays travel at the same speed and therefore both conclude that they are not moving with respect to the ether.

This result is clearly nonsensical, as Einstein points out in a lecture given at Leiden University where he had just started working in 1920.  Clearly, it is logically inconsistent if two people (Alice and Bob in our example) can be moving with respect to each other but both stationary with respect to the ether at the same time.  The resolution of this paradox is to remove the need for ether and promote light (electromagnetic fields) to a fundamental entity in the universe with no need for a medium.  To quote Einstein’s lecture

“The next position which it was possible to take up in face of this state of things appeared to be the following. The ether does not exist at all. The electromagnetic fields are not states of a medium, and are not bound down to any bearer, but they are independent realities which are not reducible to anything else, exactly like the atoms of ponderable matter.”

But the story does not end there.  To Einstein, the role that space-time played in General Relativity meant that it could be viewed as a kind of ether: empty space wasn’t really empty, it was, as we saw, a very malleable entity.

“Recapitulating, we may say that according to the general theory of relativity space is endowed with physical qualities; in this sense, therefore, there exists an ether.”

This didn’t alter the previous conclusion, this ether of General Relativity was not  a medium for electromagnetic waves.

“This space-time variability of the reciprocal relations of the standards of space and time, or, perhaps, the recognition of the fact that "empty space" in its physical relation is neither homogeneous nor isotropic  … has, I think, finally disposed of the view that space is physically empty. But therewith the conception of the ether has again acquired an intelligible content although this content differs widely from that of the ether of the mechanical undulatory theory of light.”

The idea of calling space-time “ether” was entirely idiosyncratic to Einstein.  The word was too closely tied up with being a medium for electromagnetic waves to be repurposed.  But the point that Einstein was making was an important one: that it is impossible to have truly ‘empty’ space, any region of space-time is a tangible and malleable entity.  Space and time are not abstract entities for matter to exist in.  Rather, space and time and a physical presence and can be affected by matter.   This fits perfectly with the block universe that we discussed in the previous chapter: space-time is a physical entity and cannot exist within time. It must therefore be eternal, in the sense its existence is permanent.  

We still haven’t answered why, if space-time is eternal, we perceive a flow of time.  Why can we remember the past and not the future, if both exist?  We will answer this in the following chapter.

Key Points

Mass is a form of energy.  Other forms of energy can be transformed into mass and vice versa./p>

The existence of objects with stretches space-time causing gravitation.  The existence of objects can also cause the expansion or contraction of space-time.

Footnotes

[A] To go deeper still I’ve read recently that actually the energy is not conserved.  As we’ll see in the chapter on Cosmology, empty space is filled with energy, ‘dark energy’, and since the universe is growing larger the amount of energy increases.  This continuous creation of energy means that you could in principle determine the date a video was made.  Although this means energy, as it is normally defined is not conserved, the laws of physics would still be the same at all times since the amount of dark energy is determined by the amount of space, so there is still a quantity that is conserved just not energy.  While I’m not expert enough to judge this I have trouble faulting the logic behind the reasoning.

[B] Technically the solutions to Maxwell's equations.

References

[1] On The Electrodynamics of Moving Bodies / Einstein 1905

[2] Optics in the age of Euler : conceptions of the nature of light, 1700-1795 / Casper Hakfoort.