NotesFrom a Small Universe
Ideas on space, time and causality.
The Space and Time of Albert Einstein
In this chapter we will be introduced to the Special Theory of Relativity, an elegant theory that completely transforms the way we view space and time. At the heart of it all is light and how it behaves. For something that is all around us all of the time, and so integral to how we interact with the world, science’s understanding of light came about only slowly and arduously. We will start by seeing how light was understood historically, and how it was understood as Einstein was coming to prominence. The theory that Einstein developed didn’t just expand our basic understanding of the universe, but challenged it as well: central to the theory was the idea that space and time could stretch and distort.
The Nature of Light
Young’s Double Slit Experiment
In the 1600’s and 1700’s dozens of theories to explain light were developed but they could be broadly grouped into two categories: particle theories and wave theories. Particle theories suggested that light was carried by individual particles, like tiny bearing balls, that were released in streams from light sources. Wave theories suggested that light was undulations or ripples much like a water wave on a lake.
Waves are defined by certain properties. One is that they can be superimposed. Imagine you have two water waves on a lake heading towards one another. If they are both one foot high then when the peaks of the two waves meet the waves will combine to a height of two feet. Or, if a one foot peak meets a one foot trough then the two waves will cancel out into a level surface. This additive property is known as interference. Another property of waves is that they diffract or spread out when they go through a slit. For example, a water wave will spread out when it passes through the mouth of a harbour it.
Both the particle and the wave theories of the 1700’s fell short of fully explaining all of the observed phenomena. This was in a large part because the property of interference was unknown at the time. Born in 1773, Thomas Young was the first to formulate this law. As a student, Young invested a lot of time pondering the theory of light, especially Leonhard Euler’s theory which treated light as a wave. Young went one step beyond mere pondering and often designed experiments to probe the theories. The apex of this experimentation came in 1803 which gave strong evidence to a wavelike nature of light. First, light from a source such as a lamp or the sun, is passed through a thin slit in an opaque barrier. This will cause the light to spread out as it exits the slit, something which could be attributed to either a stream of particles of to a wave. After spreading out the light hits a second opaque barrier, this time with two slits in it. The light emerging from each slit will spread out until it hits a screen. The wave theory makes a very definite prediction about what will happen in this experiment. Since the light from each slit is a series of peaks and troughs, in some places the peaks from one slit will coincide with a trough from the other slit and cancel out destructively leaving a patch on the screen with no light. In other places a peak from each slit will coincide constructing an especially bright patch of light on the screen. As it happens, this is precisely what Young saw when he carried out the experiment.
Although the light and dark bands of Young’s double slit experiment are often cited in modern textbooks as definitive proof of the wave nature of light, at the time it was met with only a lukewarm response by the scientific community, which predominantly held to a particle view of light. The lack of acceptance was partly due to the fact that the principle of interference was so novel that many did not grasp its significance. The principle of interference was developed independently by Augustin-Jean Fresnel, who later read Young’s work and went on to develop the theory further [1].
Fresnel and the Paris Academie des Sciences
It was well known that despite their popularity, particle theories of light had many deep rooted problems, and in 1817 the Paris Academie put forward an essay contest on the subject of light hoping to stimulate research [2]. Only two essays were submitted to the contest, but despite this the contest would overturn the way light was understood. One of those essays was a 140 page paper by Fresnel detailing the wave theory he had developed, the other has since been lost into obscurity. One of the contest’s judges, Simeon Poisson, noted a peculiar prediction of Fresnel’s theory: if a circular disc was illuminated at a slight angle then there would be a bright spot in the middle of its shadow. This bright central region is similar to to bright central band seen in Young’s double slit experiment, and both are a consequence of interfering waves. A second of the judges, Dominique-Francois-Jean Arago, performed the experiment and found the prediction to be true. Such a result was impossible to explain in terms of particle theories of light and Fresnel’s paper was awarded the prize, the other paper presumably settling for second place.
Fresnel’s victory in the Academie’s competition was the first step in the wave theory of light gaining widespread acceptance. Eventually the theory of the nature of light would start to become much more complicated, as we shall see in later chapters this was in part thanks to the work of Einstein himself, but this is how the theory stood when Einstein started to make his impact on the world, so this is how we shall leave it for now.
Light as an Electromagnetic Wave
During the 1800’s, huge advances had been made in the study of electricity and magnetism. There were suspicions up to this time that the two phenomena were linked; for one thing the mathematical rules governing them showed remarkable similarities and for another electrical storms were known to alter compass needles. In 1821, after decades of interest in the subject, Hans Christian Orsted was able to demonstrate a direct link between electricity and magnetism. When he held a wire carrying an electric current over a compass it caused the needle to change the direction it was pointing in: definitive proof that an electric current altered or produced magnetic fields [3].
Orsted’s discovery spurred interest in the field throughout the scientific community. One of the leaders in this research was Michael Faraday who performed many ingenious and often wonderfully simple experiments over the course of the following decades. One of the most enlightening of these experiments was when he passed an iron magnet through the inside of a coil of wire. Doing so produced an electric current in the wire but crucially only when the iron magnet was moving. This showed that a changing magnetic field produced and electric field. The culmination of all of this research was the unification of electricity and magnetism into a single phenomenon called electromagnetism. The mathematical framework of this unified force was published by James Clerk Maxwell in the mid 1850’s in a paper called On Faraday’s Lines of Forces.

James Clerk Maxwell.
The mathematical framework was complex, and still is today even after several significant simplifications have been made, so I will only give the vaguest outline of electromagnetism here. The electric force can be viewed as having the same form as a water wave on the sea. Just as a water wave has height above or below sea level at any given point, the electrical wave has a strength at any given point. Like the water wave, the strength will bob up and down, with the crest of the wave moving forward, carrying energy with it. Unlike the water wave, the electrical wave has three different directions in which to bob (the water wave simply goes up and down, the electrical wave can do this but also go sideways or forwards and backwards).
As an electric wave bobs up and down it generates a magnetic wave, which has the same wavelike form but at right angles to the electrical wave (see Figure). As the magnetic wave bobs up and down it generates an electrical wave. Since this will in turn generate a magnetic wave, the two sets of waves, electrical and magnetic, are tightly interwoven and constantly interplay with one another. Like water, electromagnetic waves have more complicated behaviour than simply moving steadily forward, they can be reflected off things or caused to swirl and eddy and form vortexes. Through these interactions, all of the attractions and repulsions of electromagnetism can be explained.
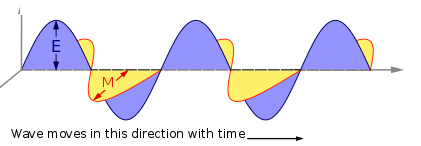
The electric and magnetic components both have the same wavelike structure but at right angles to each other. The 'height' of the electric waves are not the actual height of the wave but just represent their strength. We are used to seeing sound waves represented in this way where the height of the wave is just a scale.
Image credit: wikimedia users Parri and Jfmelero released under Creative Commons License.
In 1864, Maxwell published a further paper called A dynamical theory of the electromagnetic field. (A field, in this context, can be thought of as a set of waves, the ocean would be analogous to a water field, for example.) In this paper, Maxwell derived from the the properties of electromagnetic waves how fast they travelled. The resulting speed was in good agreement with measurements of the speed of light. From this Maxwell correctly concluded that light was a form of electromagnetic wave. In fact, Radio waves, microwaves, infrared waves, ultraviolet waves, X-Rays and Gamma-Rays as well as visible light are all types of electromagnetic radiation- perturbations in electromagnetic fields.
A quick comparison of sound and light waves
Visible light that we can see with our eyes is just a small segment on the electromagnetic spectrum (see Figure). White light is actually how we perceive light of many different visible colours arriving on our eyes simultaneously. This was demonstrated by Isaac Newton when he passed white light through a prism and separated it out into constituent colours. Although it wasn’t known then (Newton himself thought light was a particle), each different colour of light is a different wavelength, in the same way that high pitched sounds and low pitched sounds are vibrations of air with a shorter or longer wavelength. In the visible spectrum (what we can see with our eyes) red has the longest wavelength and blue (violet) has the shortest wavelength. If you took blue light and stretched it out it would gradually become redder. If you continued this process of stretching the red wave would eventually become so long our eyes would no longer be sensitive to it, it would have entered the infrared. Infrared waves were discovered when William Herschel split light through a prism and put a thermometer into the beam. Firstly, he noted that when he did so the temperature rose and that it rose to a higher temperature in the red light than in the blue light. He also saw that the temperature rose even higher if he put the thermometer next to to where the red light disappeared. This showed that there was still a form of light there even if it could not be seen. & nbsp;This also showed that light could carry energy, the infrared light was giving energy to the thermometer in the form of heat. The longer the wavelength of a wave the less energy it carries, stretching a blue wave into a red one is like pumping energy out of it. As well as its length, a wave has the property of amplitude- how high it is. Just like a sound can be loud or quiet regardless of whether it is high or low pitched, light can be of high or low intensity regardless of whether it is red or blue or completely out of the visible spectrum, such as in the radio wavelengths.
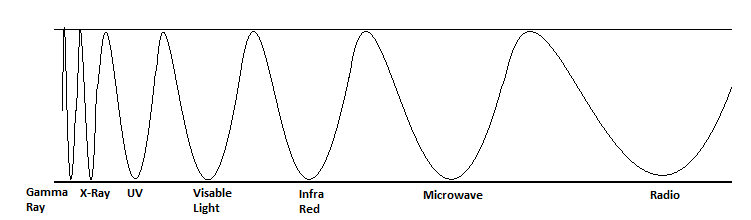
The electromagnetic spectrum. The properties of an electromagnetic wave depend upon the length of the wave. The light we see with our eyes is only a small part of the full spectrum: about 350 nanometres to 700 nanometres. We perceive different wave lengths as different colours, so we see 350 nm as blue light and 700 nm as red light.
Ether
So it was established that light had the properties of a wave in that it could diffract and interfere. But another property of a wave is that it needs a medium to carry it. A water wave, obviously, travels through water. And a sound wave travels through air. But what was a light wave travelling through- what was its medium? This was a big unanswered question by the mid 1800’s. Whatever this substance was a name was given to it: “Ether”, but no one knew anything about what properties it had. Could Ether and air be the same thing? A light wave travels through air after all. Well no, because while light can travel through space, sound can’t, the reason being that a sound wave travels through air but there is no air in space for it to travel through. So space is completely silent (as the tagline goes “In Space No One Can Hear You Scream”). But light from distant stars travels through space and reaches us here on Earth, therefore Ether had to be a different substance from air. Even if light can pass through air, the air wasn’t carrying the light wave.
Unlike a water wave, a light wave has two components, the electric and magnetic, that interact with one another in complicated ways, so right off the bat it was known that whatever the medium of a light wave was it must have a more complex structure than the medium of a water wave. A leading physicist of the time, William Thomson, developed the idea that the ether might be made of tiny molecular vortexes [4]. Most intriguingly, if Thomson’s idea was true then physical matter could be understood as condensations in the ether while light and other electromagnetic radiation could be seen as vibrations and rotations. If this programme came to fruition, all of physics could be understood as a single, unified picture. The physicist George Fitzgerald, perhaps slightly biased working as he did on electromagnetism and ether models, said Thomson’s vortex theory was “the greatest step towards the comprehension of the intrinsic theory of structure of the universe which had been made since the time of Newton” [4]. Unfortunately, this whole edifice was about to come crumbling down.
In 1887, Albert Michelson devised an elegant experiment to test for the motion of the of Earth through the ether. Since there’s ether in space, and the Earth is travelling through space as it orbits around the Sun and the Sun orbits around the centre of the Milky Way, the Earth must be moving through the ether. The effect should be an “ether wind”, the same as the passengers in an open top car experience a wind as they drive. Let’s say you manage to face into this ether wind (it doesn’t matter if you don’t know which direction it’s blowing- you can just try lots of different directions until you succeed). If you send a light wave out to a mirror in front then on its outward journey it will be travelling against the wind and on its return journey back to you, after reflecting off the mirror, it will be travelling with the wind. Now, if at the same time as you send out the first light wave you send out a second one towards a mirror off to your right. On both the outwards and return journey this second light beam will be travelling at right angles to the Ether wind so it will always have the same speed, but the first light wave will travel a little slower on its outward journey as it pushes against the wind and a little faster on its return journey as it travels with the wind. These two small differences won’t exactly cancel out; the slight gain in time the first light beam gets coming back won’t be as much as the slight loss it gets going out. So the first light beam will arrive back to you ever so slightly after the second light beam.
The Earth moves around the Sun at about 67 thousand miles per hour and the Sun moves around the centre of the Milky Way at about 483 thousand miles per hour (this second figure wouldn’t have been known to Michelson). But even these vast speeds are dwarfed by the speed of light which is about 671 million miles per hour. So the time difference between the first light beam arriving and the second light beam arriving will be absolutely tiny. But, cleverly, what Michelson set out to measure was not the time delay of the two light beams returning. Instead he measured the the brightness of the combined beams as they arrived back. We saw that a property of waves is that you can always add them together. So if the front of the two light waves arrived back at exactly the same time the brightness of the two combined would be twice as much as either wave on their own. But if the two wave fronts weren’t arriving at precisely the same time then they wouldn’t combine as strongly and the intensity of the brightness would be less than twice that of an individual wave.
This experiment was performed, many times and with great precision by Michelson and his assistant Edward Morley. What they found was was that there was no difference in the arrival times between the two light beams, the ether wind seemingly had no effect and however you were moving with respect to the ether, light appeared to have the same speed. Theorists spent a lot of effort trying to explain this result. Perhaps the Earth dragged a cloud of ether with it as it moved? Or perhaps moving against the ether wind caused objects to contract. None of the theories put forward could paint a consistent picture for all the properties of ether.
Special Relativity
What Einstein proposed was that rather than light appearing to have the same speed no matter how you moved, light actually did have the same speed no matter how you moved. This formed his Theory of Special Relativity’s first postulate (an assumption you make as the lowest level of your theory):
Postulate 1- The Speed of Light is the same for all observers, no matter what speed they have with respect to one another
and he combined this with the Galileo’s Principle of Relativity as the second postulate of his theory [A]:
Postulate 2- The Laws of Physics should be the same for any two observers who aren& rsquo;t accelerating with respect to one another.
These two rules or postulates may seem fairly innocuous or simple but, as we shall see, Einstein used them to derive an array of surprising results, which have been borne out by experiments, and which completely altered the way we look at space and time. Of course, just because it explained the Michelson-Morley experiment, doesn’t mean that we have to accept Special Relativity as true. But as we shall see now, it makes many very unique predictions which have all been verified time and again by experiment.

Albert Einstein.
Let’s remind ourselves of one of the scenarios we looked at on board Galileo’s ship. Let’s say we stand on the shore of the sea and throw a ball with enough force to make it travel at 10 miles per hour. Then we see a ship sailing past at 20 miles per hour and we see through a window our friend in the hold throw a ball with the same force as we did. Our friend would measure that ball to be travelling at 10 miles per hour, but what would we measure? We can find the speed of this ball by adding the speed of the boat, 20 miles per hour, to the speed the ball leaves our friend’s hand, 10 miles per hour, and get a total speed of 30 miles per hour.
Now let’s look at this again but using light instead of a ball and apply Postulate 1 from above. If we stand on the shore and fire off a light beam we will measure the speed of the light to be roughly 186,000 miles per second. We see a ship sail past at half this speed, 93,000 miles per second (okay, to make this just slightly more plausible maybe at this point we should decide to call it a spaceship), and we see through a window our friend in the cabin fire off a light beam. Our friend would measure this light beam to be travelling at 186,000 miles per second. And what about us? Do we measure it to be travelling at 186,000+93,000=279,000 miles per second? According to Postulate 1, no we don’t, because no matter how fast our friend in the ship is moving relative to us we must always measure the light to be travelling at 186,000 miles per second.
This has some really far reaching consequences. Imagine that we want to be able to calibrate various clocks against a certain timing instrument to make sure that they are all ticking at the same rate. Whatever design of clock we use it will of course be governed by the rules of physics, either the rules of mechanics such as Newton’s Laws and maybe the laws of electromagnetism, the specifics do not really matter.
So here is the timing instrument we decide to use to calibrate our clocks against, effectively a simple design of clock in its own right since it keeps time and we’ll call it a “light-clock”. All we have is a light beam bouncing back and forth between two mirrors. Every time the light beam bounces off the far mirror and returns back to where it started is one ‘tick’ of this clock.
Let’s say that we’re standing on the shore with a pocket watch and we time that one tick of our light-clock takes one second, conveniently. We see our friend go speeding by in their ship holding an identical pocket watch and light-clock. The beam of light in their light-clock now has further to go to complete one tick, since before all it had to do was travel to the far mirror and back, but now there is also the sideways movement of the ship to travel as well. Since the light has a constant speed of 186,000 miles per hour, the longer journey will take more time. But of course as Galileo showed, from our friend’s point of view it is the shore that is moving and the ship stays still. For them the light beam only has to travel to the far mirror and back, there is no sideways motion from the ship and so one tick of their light-clock will take one second as timed by their pocket watch. We already saw that from our point of view, stood on the shore, our friend’s light beam took longer to make its journey than our own. Since the return of their light beam coincides with a tick on their clock, our friend’s pocket watch takes longer to tick than our own. Clocks on the moving ship have slowed down.
From our friend’s point of view, as we just mentioned, the ship is stationary and it is the shore (with us on it!) that is moving. Therefore from our friend’s point of view, it is our own clocks that are running slower. The lesson here is that there is no privileged frame of reference which is ‘at rest’ compared to which all other things move, there is only movement relative to other objects and each object has its own rest frame of reference and see other things moving. The person on the ship thinks that the shore is moving and the person on the shore thinks that the ship is moving. And a moving clock always runs slower, a clock which is at rest to you will tick the fastest. This fastest-ticking clock records what is known as the “proper time”, proper in this context has the same root as “property”, i.e. the time is your property, it belongs to you, by “proper” we do not mean “more correct” as all clocks should be considered equally valid.
A common objection when coming across this argument for the first time is to say “okay, I’ll grant that maybe a light-clock will run slower when it is moving relative to me, but surely a regular pocket watch, made out of gears and wheels and all the rest, cannot behave in such a way.” But that is exactly why I mentioned that whatever design of clock we use to keep time with our light-clock, it will be subject to the laws of physics. And according to Postulate 2, the Principle of Relativity, the laws of physics must be the same no matter how fast we are moving relative to one another. So if our pocket watch keeps time with our light-clock while we are stationary then another person’s identical pocket-watch must keep identical time with their identical light-clock which is stationary to them, even if it is moving relative to us. Since the moving light-clock slows down the pocket watch must do as well.
Length Contraction
We’ve seen how Special Relativity alters the behaviour of time and now we will look at how it alters the behaviour of space, which is intertwined with time.
Let’s consider a simple way to measure a length of space which we’ve marked out with a start pole and an end pole. If we drive at a constant, known, speed then we can work out the distance we drive by the time it takes us to get between the start and end poles. For instance, if we are driving at ten miles per hour and the journey takes us one hour then we know the distance was ten miles.
Okay so let’s say our friend is driving between two poles to determine the distance by driving at a good fraction of the speed of light, starting a stopwatch when they go past the first pole and stopping the stopwatch when they go past the second pole and they work out that the time taken for the journey is 10 seconds. Meanwhile, you stand still some distance away and also set a stopwatch going when your friend’s car reaches the first pole and stop it when the car reaches the second pole. We already know that your friend’s stopwatch, since it is moving relative to you and the poles, will be running slower than your stopwatch. So if your friend timed the drive at 10 seconds you might time the drive at, say, 11 seconds.
So what can we say about the distance between the two poles if we have two different values for the time it takes for the car to drive between them? We must have two different values for the distance, of course! From your friend’s point of view the drive has taken less time and therefore the distance between the poles is shorter than the length that you measure. This effect is known as a Length Contraction.
Can Anything Travel Faster than the Speed of Light?
In fact, once we’ve accepted the first postulate, that all observers see light travelling at the same speed, it becomes logically impossible for anything to travel relative faster than the speed of light. To see this, imagine that our friend fires a light beam at a mirror some distance in front of them. Then we zip past travelling (relative to the friend) faster than the speed of light. Since our friend measures us as travelling faster than the speed of light we must overtake the light beam that they fired and therefore we can reach the mirror before the light beam does. Unable to stop in time we crash into the mirror, breaking it.
However, from our own point of view we are standing still and the light beam is of course travelling at 186,000 miles per hour so we do not catch up with it. The light beam reaches the mirror before we do it and reflects back to our friend.
Therefore, if our friend measured us travelling faster than the speed of light the mirror would be broken before the light reached it and be intact to reflect the light back. Obviously, this is not coherent, but that needn’t bother us because it shows us that nothing travels relative to anything else faster than the speed of light. (This could be proved more rigorously mathematically directly as a consequence of Special Relativity.)
One important qualifier needs to be stated here. When we talk about the speed of light we are usually talking about the speed of light in the vacuum, or in other words the speed of light in empty space. Due to light’s interactions with matter, light is slowed down when it is travelling through a medium like air or water. It is in fact possible to overtake a beam of light travelling through air, although really fantastic energies would be required and in practice only tiny, microscopic particles can achieve these speeds. I have so far omitted this qualifier for ease of writing, and will continue to do so.
Taking it to the limit
As with a lot of theories, some of the most illuminating consequences come from taking the extreme example, stretching the theory to the limits that it claims to cover and seeing what looks about to break.
Let’s return to our thought experiment of our friend travelling past us with some speed while carrying a simple light-clock. We saw that the ticking of the light-clock, and indeed all moving clocks, appeared to us to be slowed down because the light beams in the clock now had extra distance to travel- not just the distance between the two mirrors but also the distance that the mirrors themselves had moved.
Now let’s ask what happens when our friend and their light-clock are travelling past us at the speed of light. Remember that from our friend’s point of view the mirrors are stationary and the light beams are travelling in straight lines- if a light beam starts off in the dead centre of the mirrors it will bounce back and forth between the centres of the mirrors and not deviate. From our perspective the mirrors in the light-clock are travelling at the speed of light and so a light beam that’s just leaving the surface of a mirror would have to use all of its speed to travel along in the same direction as that mirror. If from our perspective the light beam crossed any of the distance between the two mirrors then it would have to be travelling faster than the speed of light, because travelling along with the mirror is travelling at the speed of light and so travelling any extra distance between the mirrors means travelling even faster.
From our perspective then, our friend’s light-clock never ticks since the light beam never travels between the two mirrors. And no other clock that our friend carries will tick either because as we saw, due to the Principle of Relativity, all the clocks they carry must march in step. So not only does our friend’s light-clock never tick but their pocket watch won’t tick either and their heart will not beat, cells in their body will not age and so on. From our perspective, as our friend reaches the speed of light, they become frozen in time.
And how do things appear from the perspective of our friend? Let’s look again the experiment where our friend drives between a start pole and an end pole with a stopwatch running in order to measure the distance between them, only this time with our friend driving at the speed of light. If the light beam has just left the surface of one mirror as they pass the start pole then it will still be in the exact same place, no matter how small the distance between the mirrors is the light-clock will never tick once during the drive between the two poles. Thus, from our friend’s point of view, the drive takes zero time which means they calculate the distance between the poles as being zero. For a person moving at the speed of light all events (such as the event of driving past the the start pole and the event of driving past the end pole) happen at the same time. And for a person moving at the speed of light any two points in space on the path that they travel (such as the start line and the finish line) have zero distance between them and exist on top of each other. Of course, since thinking and being aware of the world is to some extent a physical process (it relies on physical interactions within the brain) a person moving at the speed of light wouldn’t actually be able to perceive any of this so no conscious observer could travel between points in space at the speed of light. So although it is sometimes useful to talk about what the world looks like when travelling at the speed of light, it is important not to take the suggestion too much at face value.
What is Space?
It seems that we have an inbuilt view of space as a three-dimensional (up-down, left-right and forward-backward) entity that exists independently of us as humans or any material constructs that might be embedded in space and if all of the material universe were to suddenly disappear then space would carry on regardless, only empty. It seems obvious that in light of the results of Special Relativity that this intuitive view has to change in some way. How can there be a definite measure of space if a person stationary on the Earth would say “there are four feet of space between those buildings” but a person travelling past the Earth at a fast speed would say “there are two feet of space between those buildings”?
We can no longer have an absolute measure of space that exists independently of the matter in the universe, we can only have amounts of space relative to other things. So for the person stationary on the Earth, the buildings do not have two feet of space between them because space isn’t something that can be measured. All that can be said is that if you had a measuring rod defined as one foot in length and placed it at the base of one of the buildings, the length between the buildings would be twice the length of the measuring rod. For the person travelling at speed the length between the buildings is still twice the length of the same measuring rod, i.e. the one placed on the ground between the buildings.
This idea is called Mach’s Principle of Space, after Ernst Mach: there is no such thing as an independent, absolute space, the only meaningful measure is the distance between objects. If all of the objects in the universe disappeared then there would no longer be such a thing as space.

Ernst Mach.
What is Time?
As with space, I think that from an early age we all develop a very similar intuitive view of time. We all feel we know what time is even if it is very hard to describe, although I will attempt to here. I think the intuitive view of time is that the only thing that is real is the present which is constantly changing. A line representing time could be drawn on a page and for any instant of time a godly observer outside the universe could put their finger on the line and say “This point here is the present time” and according to our human experiences that finger would have to move steadily along the line.
But again, in view of the results of Special Relativity I think that this intuitive view of time becomes untenable. To take an extreme example, what about a person who, at the beginning of human history, is travelling at the speed of light. To that person all the events of human history happen at the same time while for a person stationary on the surface of the Earth there are thousands of years between them. How can there be such a thing as “the present”, the point on the line with the fingertip on it, if for the travelling person that present contains all of human history but for the stationary person that present contains just the tiniest fraction?
And again, we need a shift in perspective to thinking of time as a relative quantity. Just as the distance between two points should not be thought of as being measured in absolute space, the time between two events should not be thought of as being measured in absolute time.
Obviously I am trying to make an analogy between space and time here. But all analogies break down at some point. After all, space and time may have many similarities but they are not one and the same. Consider this problem:
What if you had a clock but you did not know if it was keeping time correctly. How would you find out? You could hold it next to another clock and see if they run at the same speed. But maybe this second clock was not keeping time? Perhaps both clocks are wrong but you could not tell because they were equally wrong. You could take both clocks and compare them to a third clock and so on. Even if you could compare all of the clock in the universe (and we use the term ‘clock’ broadly here, we could include your pulse and a swinging pendulum as well) you would only be able to say that they kept time with one another. But actually this is enough, as long as they all kept time relative to each other does it matter if they collectively slow down or speed up? What would that even mean?
For practical purposes the turning of the Earth is a clock, i.e. the length of a day. Of course this was the standard measure of time before mechanical clocks were invented (and how would you know that these were keeping time? By comparing the clock’s time with the time of day). Anything moving regularly with the turning of the Earth could be considered as a clock.
This definition of a clock is relativistic because if all of human history took one hundred thousand days as measured by people on the Earth it would also take one hundred thousand days (one hundred thousand rotations of the Earth) as measured by a fast moving person outside of the Earth.
Using the movement of the Earth in this way seems kind of arbitrary but what I’m really trying to say is not that we should use the movement of the Earth as the standard clock but that we should use movements in space to measure time. If we want to know the duration of an event we want to know how long something takes to change. We cannot measure how long it takes to change in absolute time so we ask how long it takes to change relative to how much everything else in the universe changes relative to one another. When we say that a clock that is travelling relative to us at the speed of light has stopped ticking (stopped changing!) what we mean is that it no longer changes even though other things in the universe change. Just as if all the matter disappeared there would be no such thing as space, also there would there be no such thing as time, because time is just a measure of things changing relative to one another in space. In analogy to the Machian view of space we can call this idea Machian Time.
Simultaneity- Shutting the barn door while the horse is bolting
The sections above tell us that conceptions of space and time are deeply connected to individuals: two different people can see the space and time connecting two events as being quite different. We will see now that in Special Relativity not only do different people not always agree on the duration between events, but they do not always agree on what constitutes the ‘present’ (i.e. what is happening right now). This will ultimately give us great insight into what the nature of space and time are.
Let’s revisit our friends Alice and Bob. Let’s say that Alice is a stunt pilot and for one of her stunts she wants to fly her plane straight through a barn with a large door on each side. Meanwhile, Bob will be stood outside the barn and use a lever to open and shut the barn doors. As part of the trick, Alice wants there to be an instant when both doors are shut with the plane sealed inside the barn before the exit door opens allowing her to fly out. Unfortunately, when she parks the plane next to the barn she sees that the plane and the barn are exactly the same length meaning that there is not enough room inside for both doors to be shut at the same time.
" Don’t worry,” Bob tells her. “Your plane will be travelling pretty fast when it flies through and this means that it will be length contracted. Therefore the plane will just fit inside the barn with both doors shut and an instant later I can open the exit.”
Alice think this is fine and they carry out the stunt. Just as she is entering the barn a terrible thought strikes her: from her perspective she is at rest and the barn is travelling towards her. This means that the barn is length contracted and so her plane won’t fit inside. Surely she will be crash into one or other door?
Is Alice right to be worried? How can Bob think she will fit but Alice think she won’t?
We know from our discussion above that observers moving with respect to one another won’t experience time in the same way. Not only do they not agree on the duration of events (time dilation) but they will also not agree on whether two events happen at the same instant (whether or not they are simultaneous).
For Bob (and any spectators on the ground), the two barn doors will indeed be closed for an instant, with Alices length-contracted plane fitting snugly inside. For Alice, the entrance door shuts momentarily after the exit door opens for her and at no instant is her plane sealed inside the length-contracted barn.
Moving observers do not always agree on the order that events happen in. However, and very importantly, if one event causes another event, they will both agree on which event came first. In this example, Bob pulling the lever causes the barn doors to trigger. This means that all observers, no matter how they are moving relative to one another, will agree the lever was pulled before either door triggers even if they don’t agree on how long there is between the lever being pulled and each door triggering.
Why? Because all observers agree that light travels at the same speed. In order for one event to cause another a signal must pass between them. In this example, a signal must be passed from the lever to the barn doors. This signal could move at the speed of light (e.g. triggering a light sensitive sensor on the doors) or slower (e.g. firing a bearing ball into the door).
For simplicity, let’s say that when Bob pulls the lever a light ray is sent out in each direction and when these hit a sensor located on each door they close. Bob is in the middle of the two doors and light travels in each direction at the same speed and therefore the two doors close at the same time. Alice is flying towards the barn at 100 mph although of course from her point of view she stays still and the barn moves towards her. Therefore the near door of the barn is moving away from the light source and the far door of the barn is moving towards the light source [B]. Since both light rays must move at the same speed, the far barn door, moving towards the source of the rays, will trigger before the near door which is moving away from the rays (see Figure ). This agrees with what we worked out above, from Alice’s point of view the far door (the exit) shuts then reopens a tiny bit before the near door (the entrance) shuts.
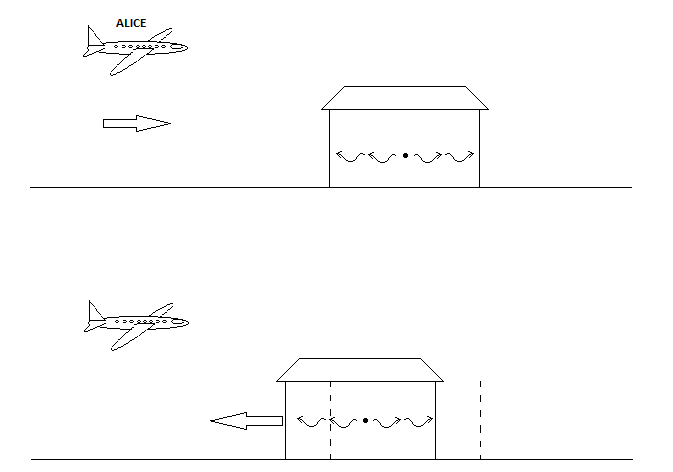
Top: From Bob's point of view, Alice is moving but the barn stays still. The light moves in both directions at the same speed and so both walls are hit at the same time.
Bottom: From Alice's point of view, she is staying still but the barn moves towards her. The light still moves in both directions at the same speed but the far wall, which is moving towards the light source, is hit before the rear wall, which is moving away from it.
Present Understanding
Let’s examine the point in the trick where Alice is in the dead centre of the barn, level with Bob who is outside.
At this point Bob, who is moving relative to Alice, would say that “at present both barn doors are shut” whilst Alice would say “at present the exit door is shut but the entrance door has not shut yet”. The key thing here is that anyone who is moving relative to others will have their own definition of the present: their own configuration of matter in the universe which they could claim currently exists.
Here is an interesting thing. From Alice’s point of view the entrance door shutting has not yet happened but from Bob’s point of view it already has happened. Even though Alice considers that event to be in the future it is predetermined. She might not know it, but from Bob’s perspective it has already occurred and so it must also occur from her perspective as well.
How can we rectify everyone having their own definition of the present? If I run past you, then at the instant we meet you are in my present instant, I am in your present instant but other than that we have completely different ideas of the present. This is only possible we we consider all of space-time as existing in an eternal fashion, without the passing of time, known as a block universe. The ideas of a past or a future, or even the passing of time itself, only make sense to us as beings inside space-time. Each person has their own three-dimensional present moment, which are different views through a four-dimensional, unchanging universe [C].
Furthermore this is the only way we can make sense of the fact that in, our example above, for Alice some events were predetermined to occur, since they had already occurred for Bob. Fundamentally there was no passing of time, all of it was predetermined for both Alice and Bob,but they experience what is ‘present’ in different ways.
It is all well and good to claim that space-time is eternal. But it leaves many questions unanswered. Such as what are space and time? What is the physical nature of this eternal, four-dimensional block universe? Why do we have memories of the past and not the future, if time does not really flow?
We will tackle all of these questions in due course. In the next chapter, we will look at how Einstein’s theory of General Relativity gives us our best understanding of the physical nature of space-time. Then we will go on to see how we understand causality and the flow of time from our theory of the universe on the scale of microscopic particles called quantum mechanics.
Key Points
Even though light is a wave it doesn’t have a medium to carry it in the same way as water waves or sound waves. Light is a fundamental entity in the universe.
Different people won’t necessarily agree on the absolute distances between objects or time intervals between events. They will only agree on the relative distances and time intervals. This means that our conceptions of space and time are Machian: we define distances in relation to the length of other objects and time intervals in relation to the duration of other events.
Footnotes
[A] On a technical note, it has been pointed out to me that the first postulate can be considered part of the second postulate since the speed of light for any observer can be derived from Maxwell’s equations.
[B] Because the near door moves away the light must travel further in total to reach it. Light travels the same speed in both direction. More distance at the same speed means a longer time.
[C] For further reading see the Rietdijk-Putnam Argument.
References
[1] Optics after Newton : theories of light in Britain and Ireland, 1704-1840 / G.N. Cantor.
[2] Convolutions in French Mathematics 1800-1840, Volume II Section 13
[3] Electricity and Magnetism: A Historical Perspective / Brian Scott Baigrie